| Ιστορικά |
| Το πολυώνυμο Jones ανακαλύφθηκε το 1984 από τον Vaughan F. R. Jones. Σε αντίθεση με το πολυώνυμο Alexander, το πολυώνυμο Jones μπορεί να διακρίνει ένα κόμβο από την κατοπτρική του εικόνα. Το πολυώνυμο Jones είναι περίπου το ίδιο με το πολυώνυμο Kauffman bracket όπως θα δούμε παρακάτω. |
| Κανόνες Ορισμού |
| Το πολυώνυμο Jones δημιουργείται από ένα προσανατολισμένο διάγραμμα κόμβου μέσω τριών βασικών κανόνων: |
| • Είναι αναλλοίωτη ισοτοπίας |
| • VU(t) = 1 |
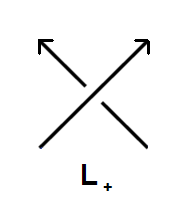
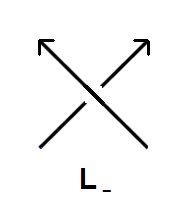
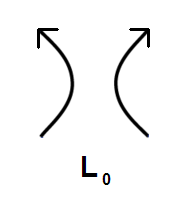
| • t-1 · VL+(t) - t · VL-(t) = (t1/2 - t-1/2) · VL0(t) |
| Ο δεύτερος κανόνας λέει ότι το πολυώνυμο Jones για τον τετριμμένο κόμβο είναι η μονάδα. Ο τρίτος κανόνας για τον υπολογισμό του πολυωνύμου Jones είναι οι σχέσεις skein. Οι όροι VL+(t), VL-(t) και VL0(t) αντιστοιχούν στα πολυώνυμα τριών διαγραμμάτων L+, L-, L0 τα οποία διαφέρουν μόνο κατά την περιοχή μιας διασταύρωσης, όπως παρακάτω. |
|
|
|
| Υπολογισμοί |
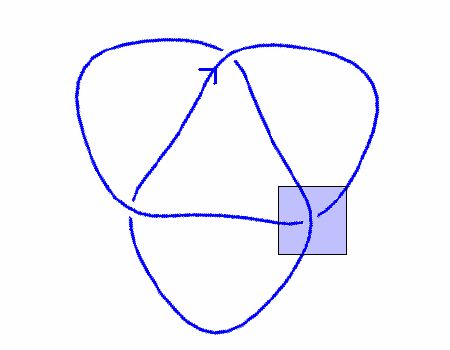
| Το πρώτο βήμα για να ξεκινήσουμε με τον υπολογισμό του πολυωνύμου Jones ενός προσανατολισμένου κόμβου είναι η επιλογή μιας διασταύρωσης σε ένα διάγραμμα του κόμβου την οποία επιλέγουμε είτε ως L+ είτε ως L-. Στο παράδειγμα του δεξιόστροφου κόμβου trefoil έχουμε επιλέξει μια διασταύρωση L-. |
|
|
Η σχέση skein τότε γίνεται: VL-(t) = t-1 · VL+(t) / t - (t1/2 / t - t-1/2 / t) · VL0(t) |
| Η επιλεγμένη διασταύρωση αλλάζει στα άλλα δυο διαγράμματα L+ και L0. Στην περίπτωση του L+ με μια κίνηση RII ακολουθούμενη από μια κίνηση RI οδηγούμαστε στον τετριμμένο κόμβο. Έτσι η τιμή του VL+(t) γίνεται 1. |
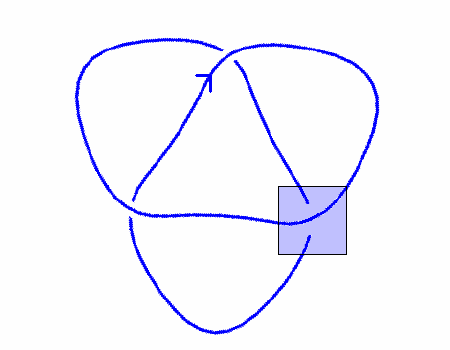
|
| VL+(t) = 1 |
| Στην περίπτωση του L0 οδηγούμαστε στον προσανατολισμένο κρίκο Hopf (Hopf link) και μετά από πράξεις στο αποτέλεσμα: |

|
| VL0(t) = -t - t-1 |
| Αντικαθιστώντας αυτές τις τιμές στην αρχική σχέση skein παίρνουμε το τελικό αποτέλεσμα για το πολυώνυμο Jones του δεξιόστροφου κόμβου trefoil. |
| VL(t) = t-1 + t-3 - t-4 |
| Ανοικτό Πρόβλημα |
| Υπάρχει μη τετριμμένος κόμβος Κ με VK[t] = 1 ; |
| Προηγούμενη Ενότητα | Επόμενη Ενότητα |