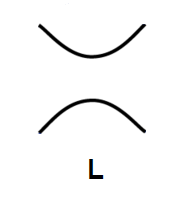|
|
|
Ιστορικά
|
|
|
|
Το 1985 ο L. H. Kauffman ανακάλυψε το δικό του πολυώνυμο το οποίο είναι συναφές με το πολυώνυμο Jones, το πολυώνυμο bracket. Το πολυώνυμο bracket δεν είναι αναλλοίωτη πλήρους ισοτοπίας αλλά είναι αναλλοίωτη κανονικής ισοτοπίας, δηλαδή μόνο ως προς τις κινήσεις RIΙ και RIΙΙ. Ο Kauffman όμως βρήκε μια μαθηματική έκφραση την οποία πολλαπλασιάζοντάς την με το πολυώνυμο bracket ενός κόμβου έπαιρνε το πολυώνυμο Jones του κόμβου.
|
|
|
|
|
|
|
|
Κανόνες Ορισμού
|
|
|
|
Το πολυώνυμο bracket δημιουργείται από ένα μη προσανατολισμένο διάγραμμα κόμβου. Το bracket για ένα διάγραμμα υπολογίζεται χρησιμοποιώντας τους παρακάτω τρεις κανόνες:
|
|
|
|
• < U > = 1
|
|
|
|
• < DU > = (A2 + A-2) · < D >
|
|
|
|
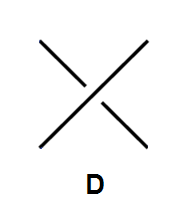
• < C > = A · < L > + A-1 · < R >
|
|
|
|
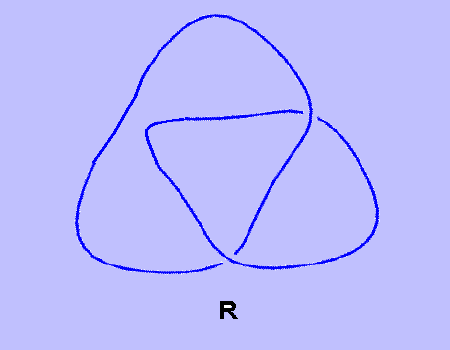
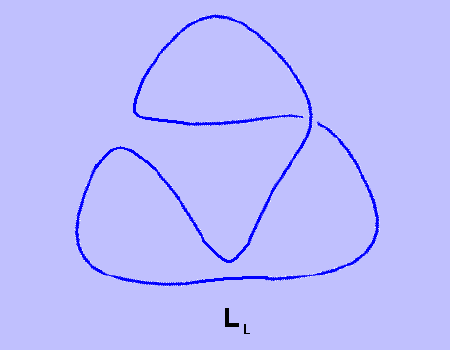
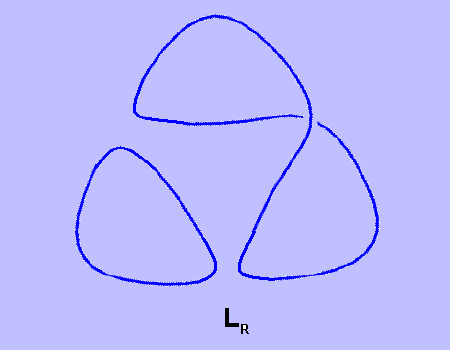
όπου το < U > συμβολίζει το bracket του τετριμμένου κόμβου, το DU αναφέρεται στον διαχωρίσιμο κρίκο που αποτελείται από ένα διάγραμμα D και τον τετριμμένο κόμβο και τα < D >, < L > και < R > αναφέρονται στα πολυώνυμα των διαγραμμάτων που διαφέρουν μόνο στην περιοχή μιας διασταύρωσης όπως παρακάτω.
|
|
|
|
|
|
< D > = A · (A · < LL > + A-1 · < LR >) + A-1 · < R >
|
|
|
|
Μετά από διεξοδική ανάλυση φτάνουμε στο ακόλουθο πολυώνυμο bracket για τον αριστερόστροφο κόμβο trefoil.
|
|
|
|
< K > = A7 - A3 - A-5
|
|
|
|
|
|
|
|
Συμπέρασμα
|
|
|
|
Εφ' όσον το πολυώνυμο bracket είναι μια αναλλοίωτη κανονικής ισοτοπίας, δεν μπορούμε να απλοποιήσουμε σε ένα διάγραμμα τις κινήσεις RI. Αυτό οδηγεί σε εξαντλητική ανάλυση των διαγραμμάτων. Όμως μπορεί να κατασκευαστεί αναλλοίωτη και υπό την κίνηση RI μέσω του bracket με την παρακάτω εξίσωση.
|
|
|
|
f[L] = (-A)-3 · w(D) · < D >
|
|
|
|
Σ' αυτή την εξίσωση το w(D) είναι ο αριθμός συστροφής, (writhe) του κόμβου, δηλαδή το άθροισμα όλων των προσήμων των διασταυρώσεων του D, αφότου έχουμε δώσει στο D προσανατολισμό. Θέτοντας όπου Α το t-1/4 παίρνουμε f[L](t-1/4) = VL(t) δηλαδή παίρνουμε το πολυώνυμο Jones.
|
|
|
|
|