| Ιστορικά |
| Η δημοσίευση του πολυωνύμου Jones ενθουσίασε τη μαθηματική κοινότητα σε βαθμό που δημιουργούνταν καινούργιες πολυωνυμικές αναλλοίωτες πολύ γρήγορα. Στόχος της εποχής ήταν να βρουν μια πολυωνυμική αναλλοίωτη η οποία θα γενίκευε το πολυώνυμο Alexander και το πολυώνυμο Jones. Το πολυώνυμο HOMFLYPT ήταν μια επιτυχημένη λύση η οποία δημοσιεύθηκε ταυτόχρονα από διαφορετικές ομάδες μαθηματικών. Η εργασία δημοσιεύθηκε υπό τα ονόματα των Hoste, Ocneanu, Millett, Freyd, Lickorish, Yetter, Przytycki και Traczyk. Το πολυώνυμο HOMFLYPT χρησιμοποιεί σχέσεις skein όπως και τo πολυώνυμo Jones και το πολυώνυμο Alexander, όμως το καινούργιο πολυώνυμο χρησιμοποιεί δυο μεταβλητές σε αντίθεση με το πολυώνυμο Alexander και το πολυώνυμο Jones, και για κατάλληλες τιμές εξιδεικεύεται στο καθένα από αυτά. |
| Κανόνες Ορισμού |
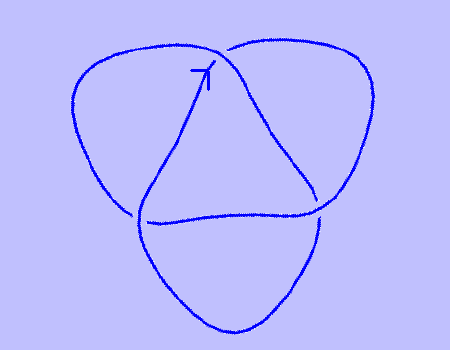
| Το πολυώνυμο HOMFLYPΤ δημιουργείται από ένα προσανατολισμένο διάγραμμα κόμβου όπως το παρακάτω. |
|
| Επίσης, το πολυώνυμο HOMFLYPΤ υπολογίζεται χρησιμοποιώντας σχέσεις skein όπως και το πολυώνυμο Jones. Οι κανόνες του πολυωνύμου είναι οι εξής. |
| • P(L) είναι αναλλοίωτη ισοτοπίας |
| • P(U) = 1 |
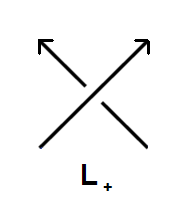
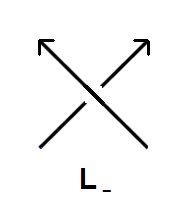
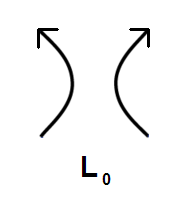
| • l · P(L+) + l-1 · P(L-) + m · P(L0) = 0 |
| με την ίδια σύμβαση για τα L+, L-, L0, όπως και στο πολυώνυμο Jones. |
|
|
|
| Υπολογισμοί |
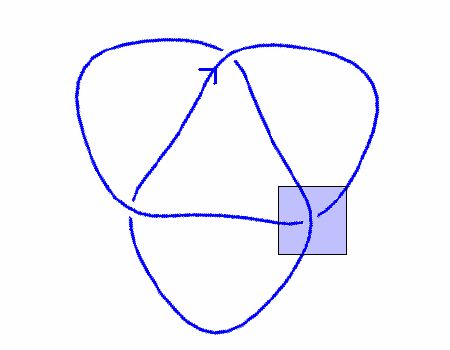
| Για να υπολογίσουμε το πολυώνυμο HOMFLYPT, επιλέγουμε μια διασταύρωση και εφαρμόζουμε τη σχέση skein για τα πολυώνυμα των τριών διαφορετικών διαγραμμάτων. Στο παρακάτω παράδειγμα έχουμε επιλέξει μια διασταύρωση τύπου L-. Έτσι λύνουμε τη σχέση skein ως προς τον όρο P(L-). |
|
| P(L-) = -l · (l · P(L+) + m · P(L0)) |
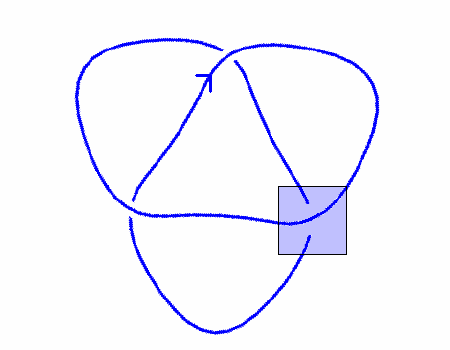
| Παρακάτω απεικονίζεται το διάγραμμα L+. |
|
| Λόγω του πρώτου κανόνα το διάγραμμα του κόμβου μπορεί να απλοποιηθεί όταν φθάνουμε σε ισοτοπικό του τετριμμένου ή άλλων γνωστών κόμβων. Πράγματι, έτσι μπορούμε να πάρουμε τον τετριμμένο κόμβο αν μετά από μια κίνηση RII χρησιμοποιήσουμε μια κίνηση RI. Από το δεύτερο κανόνα το πολυώνυμο του τετριμμένου κόμβου είναι 1, έτσι και η τιμή του P(L+) είναι 1. |

|
| P(L+) = 1 |
| Στην περίπτωση του L0, με κάποια απλοποίηση του διαγράμματος οδηγούμαστε στον κρίκο Hopf, και μετά από πράξεις οδηγούμαστε στο P(L0). |

|
| P(L0) = -lm + l3m-1 + lm-1 |
| Αντικαθιστώντας τα αποτελέσματα στην αρχική σχέση skein παίρνουμε το τελικό αποτέλεσμα για το πολυώνυμο HOMFLYPΤ του δεξιόστροφου κόμβου trefoil. |
| P(L) = l2m2 - 2 · l2 - l4 |
| Συμπέρασμα |
| Το πολυώνυμο HOMFLYPΤ είναι μια πιο γενική αναλλοίωτη, η οποία εξειδικεύεται και στο πολυώνυμο Alexander και στο πολυώνυμο Jones. |
| Προηγούμενη Ενότητα | Επόμενη Ενότητα |