| Μια διαπλοκή (tangle) είναι οποιαδήποτε περιοχή ενός διαγράμματος κόμβου η οποία μπορεί να περιβληθεί από έναν κύκλο, έτσι ώστε ο κύκλος να διασταυρώνει τον κόμβο σε τέσσερα σημεία. Δύο διαπλοκές είναι ισοτοπικές ή τοπολογικά ισοδύναμες εάν με μια ακολουθία από κινήσεις Reidemeister μπορούμε από τη μια να έχουμε την άλλη, πάντα υπό την προυπόθεση πως η διαπλοκή παραμένει μέσα στον κύκλο κατά τη διάρκεια των κινήσεων Reidemeister. |

|
| Παρακάτω μπορούμε να δούμε κάποιες ειδικές περιπτώσεις. Ένα ζεύγος από μη τεμνόμενες κάθετες γραμμές ονομάζεται [ ∞ ] διαπλοκή, ένα ζεύγος από μη τεμνόμενες οριζόντιες γραμμές ονομάζεται [ 0 ] διαπλοκή και ένα ζεύγος από γραμμές οι οποίες διασταυρώνονται 3 φορές ονομάζεται [ -3 ] διαπλοκή. Εάν η περιστροφή ήταν δεξιόστροφη αντί για αριστερόστροφη τότε θα ονομαζόταν [ 3 ] διαπλοκή. |

|

|

|
||
| [ ∞ ] tangle | [ 0 ] tangle | [ -3 ] tangle |
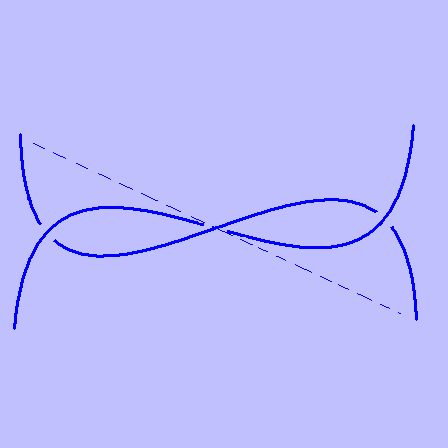
| Μπορούμε να χρησιμοποιήσουμε αυτόν το συμβολισμό για να χαρακτηρίσουμε πιο περίπλοκες διαπλοκές. Για παράδειγμα παρακάτω έχουμε αρχικά μια [ -3 ] διαπλοκή (α). Μετά από μια ανάκλαση ως προς τη διακεκομμένη γραμμή παίρνουμε το επόμενο διάγραμμα (β). Έπειτα περιστρέφουμε τα δύο δεξιά άκρα και παίρνουμε τη διαπλοκή [ -2, -3 ] (γ). Στη συνέχεια κάνουμε ακόμα μια ανάκλαση (δ). Όπως βλέπετε, πάντα εργαζόμαστε στη δεξιά πλευρά της διαπλοκής. Στη συνέχεια περιστρέφουμε κατά την αρνητική φορά τα δύο δεξιά άκρα 4 φορές (ε). Έτσι, το αποτέλεσμα έχει συμβολισμό Conway [ 4, -2, -3 ]. |
|

|

|

|

|
||||
| (α) | (β) | (γ) | (δ) | (ε) |
| Διαπλοκές που κατασκευάζονται με αυτόν τον τρόπο λέγονται ρητές διαπλοκές. Μπορούμε να χρησιμοποιήσουμε τους παραπάνω αριθμούς για να δημιουργήσουμε ένα συνεχές κλάσμα. Δουλεύουμε με φορά από δεξιά προς τα αριστερά και έχουμε το εξής συνεχές κλάσμα που σχετίζεται με το [ 4, -2, -3 ]: |
| 4 + ( 1 / ( ( -2 ) + 1 / ( -3 ) ) ) |
| Εάν το απλοποιήσουμε παίρνουμε το κλάσμα 25/7. |
| Ισχύει το ακόλουθο θεώρημα (Conway, 1970): Υπάρχει μια αμφιμονοσήμαντη και επί αντιστοιχία ανάμεσα στις κλάσεις ισοτοπίας των ρητών διαπλοκών και στο σύνολο QU{∞}. |
| Προηγούμενη Ενότητα | Επόμενη Ενότητα |