ΜΗ ΓΡΑΜΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ

 Download

ΑΣΚΗΣΕΙΣ

   1. Να δειχθεί ότι η εξίσωση  έχει ακριβώς μια ρίζα  στο διάστημα [1,2]. Να γίνουν 3    

       επαναλήψεις της μεθόδου της διχοτόμησης. Πόσες επαναλήψεις πρέπει να γίνουν ώστε

       ;

   2. Η συνάρτηση  έχει αντίθετα πρόσημα στα σημεία 0 και 1. Ποιό σημείο εντοπίζει η

       μέθοδος της διχοτόμησης αν εφαρμοστεί στο διάστημα [0,1]; Είναι αυτό το σημείο ρίζα της        

       ;

   3. Η εξίσωση  έχει μια μοναδική ρίζα  στο [0,1]. Να δειχθεί ότι η γενική

       επαναληπτική μέθοδος  συγκλίνει στη ρίζα αυτή για οποιοδήποτε  στο

       [0,1]. Να γίνουν 3 επαναλήψεις με  και να δοθεί μια εκτίμηση του σφάλματος .

       Επίσης, θέτοντας , να δειχθεί ότι  όταν

   4. Να δειχθεί ότι η ακολουθία , με , συγκλίνει στο 1 γραμμικά και ότι η ακολουθία ,

       με , συγκλίνει στο 1 τετραγωνικά.

   5. Έστω και  μια λύση της εξίσωσης  στο [a,b].        

       Έστω επίσης η γενική επαναληπτική μέθοδος   με  Να δειχθεί ότι,

       αν  τότε η ακολουθία  συγκλίνει στο  μονότονα, ενώ αν

        τότε η  συγκλίνει στο  και το  βρίσκεται πάντα μεταξύ δύο διαδοχικών

       επαναλήψεων.

   6. Έστω η εξίσωση . Υποθέτουμε ότι  και ότι η εξίσωση αυτή έχει μια ρίζα .

       Γράφοντας την εξίσωση αυτή στην ισοδύναμη μορφή ,

       να βρεθούν οι τιμές του  για τις οποίες η επαναληπτική μέθοδος   δεδομένο,

       συγκλίνει για  αρκετά κοντά στο . Για ποιά (θεωρητική) τιμή του  η σύγκλιση είναι    

       υπεργραμμική;

    7. Να δειχθεί ότι η επαναληπτική μέθοδος , με , συγκλίνει στην μοναδική ρίζα 0

       της εξίσωσης , για κάθε αρχικό  (και άρα για κάθε , γιατί;), παρόλο που

       δεν ισχύει η συνθήκη  (αφού έχουμε εδώ ). Αντίθετα, να δειχθεί ότι η

       επαναληπτική μέθοδος, με , δεν συγκλίνει για κανένα αρχικό  στη μοναδική ρίζα

       0 της εξίσωσης , και ότι πάλι δεν ισχύει η συνθήκη .

    8. Έστω η εξίσωση . Να εφαρμοστεί η μέθοδος Newton-Raphson για την εύρεση

       μιας προσέγγισης  της ρίζας  της εξίσωσης αυτής τέτοια ώστε να ισχύει . Ο    

       εντοπισμός του αρχικού σημείου  να γίνει γραφικά.

    9. Ο αντίστροφος ενός αριθμού μπορεί να υπολογιστεί χωρίς διαίρεση από τον αλγόριθμο

        a)   Να δειχθεί ότι η σχέση αυτή προκύπτει από την εφαρμογή της μεθόδου Newton Raphson

        στην εξίσωση . Για ποιες αρχικές τιμές η ακολουθία  συγκλίνει;

        b)  Με , να γίνουν 2 επαναλήψεις για να υπολογιστεί μια προσέγγιση του αντίστροφου του

        αριθμού 4 με τη μέθοδο αυτή.

    10. Η εξίσωση  έχει μόνο μια πραγματική ρίζα και μάλιστα η ρίζα αυτή βρίσκεται στο

        διάστημα (2,3). Αποδείξτε αναλυτικά ότι, αν , τότε η ακολουθία  που παράγει η μέθοδος

        Newton-Rapshon συγκλίνει στη ρίζα . (Υπόδειξη: Δείξτε ότι η ακολουθία , , είναι

        φθίνουσα και κάτω φραγμένη).

   11. Να εφαρμοστεί η μέθοδος της Τέμνουσας για την εύρεση της ρίζας της εξίσωσης  με   

         (δύο επαναλήψεις).

    12. Να εφαρμοστεί η μιγαδική μέθοδος Newton-Rapshon στην εξίσωση  (τρεις

         επαναλήψεις, με ).

    13. Να εφαρμοστεί η μέθοδος Newton-Raphson στο μη γραμμικό σύστημα

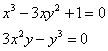
         με  (μία επανάληψη).